3D imaging used in dentistry. Once a panoramic x-ray is taken, the technician uses software to rotate the image; the software uses matrix mathematics to compute the position of the rotated image.One use for matrix math is in programming 3D engines for video games. A single point on the screen can be defined as a vector. The TV or computer screen is two-dimensional only, so to create the look of depth, objects must change size as they come closer to the viewer or go farther back into the scene. An image is made up of hundreds or thousands of vectors. By multiplying this set or matrix, you can change its size. You can also multiply the vector array by another array, which allows you to rotate the image. In rotation, parts of the image become larger and some become smaller as the image rotates about an axis.
The 3D imaging in games is now crossing into medical imaging technology. Instead of a game programmer designing an initial object, for example, a medical scan inputs data for an organ or blood vessel. The software can then rotate and present the organ or blood vessel from different angles. The same imaging technology can scan a water pump in a nuclear plant and present the operator with a movable 3D image of a part of the pump.
Imagine for a moment that you are a mechanical engineering technologist who has specialized in the area of non-destructive evaluation of engineered parts. (There are courses and complete programs at some colleges in becoming an NDE specialist.) Your company is looking into a software package that will render three-dimensional images of parts scanned using ultrasonic sound waves. Your department manager believes that some of the older mechanical engineer managers and vice-presidents you have for clients will want to know how 3D imaging works. As a recent college graduate, you are expected to know about computers and programs. You will need to do a brief presentation on how the program can take scanned input and produce a 3D image that can then be rotated and examined from all sides. Here we will prepare the last part of the seminar on the rotation of the image, using matrix mathematics.
When doing a presentation to clients, senior managers or professionals, you have to remember that they have been involved with specialty areas or administration for a while, so you want to keep it straightforward without being too basic and causing insult. It can be a little tricky. Be diplomatic and don’t take offence if they ask you to skip ahead (it’s a good idea to let the audience know that you are ready to skip ahead if they would like).
The basic concept here is that a matrix can use four elements to represent a three-dimensional point in space by expressing the three angles from the \(x\), \(y\), and \(z\) axes and the lengths of the vectors. Then, by multiplying by the sine, cosine, or tangent of the angles, you can rotate the matrix about one of the axes. Here are examples of matrices that can be used.
| To rotate along the \(x\)-axis: |  |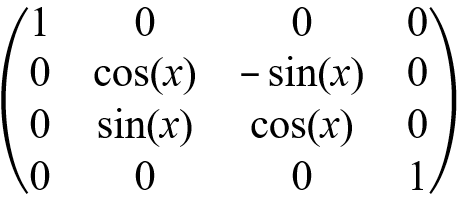
| To rotate along the \(y\)-axis: | |
| To rotate along the \(z\)-axis: | |
For example, to rotate a matrix along the \(x\)-axis, you would compute the following:
To the right of the equation, we have the rotation matrix multiplied to the vector matrix containing information about a single vector mapped to a specific location on the 3D image. Of course, to rotate the entire 3D image, this would be applied concurrently to every vector mapped to the digital image being analyzed (in theory, each vector would have a unique set of elements).
To rotate a single vector of length 1 by 60° (i.e. \(\theta = \frac{\pi}{3}\) radians) along its \(x\)-axis, where the vector has \(x\), \(y\), and \(z\) components of 45°, 45°, and 90° from their reference axes, respectively, the matrix multiplication statement would look like this:
Notice how the angle relative to the \(x\)-axis did not change (remained as \(\frac{\pi}{4}\)), while elements in row 2 and 3 changed. A similar occurrence happens had we rotated along the \(y\)-axis, except with rows 1 and 3 changing instead.
You can also find matrices for translation (movement along an axis) or for scaling an image. To see this math performed on a 2D image, watch this basic tutorial found on our YouTube channel linked below:
